Including demographic processes in a population model
Jian Yen
5/11/2020
Source:vignettes/including_processes.Rmd
including_processes.RmdDemographic processes?
This is a broad term that could mean many things.
aae.pop focuses on four main processes:
demographic stochasticity: random variation in the outcomes of individual processes (e.g. birth, death), resulting in variation in population abundances.
environmental stochasticity: random variation in external conditions, resulting in variation in the vital rates (i.e., the population matrix).
density dependence: variation in vital rates or population outcomes that depends on the abundance of the population. Density dependence can be negative (e.g., due to limited resources) or positive (e.g., Allee effects).
covariate effects: the influence of covariates on the population matrix. In
aae.pop, covariate effects are included primarily to allow the population matrix to change through time in response to external factors (e.g., weather, habitat availability).
Two additional processes, dispersal and interspecific interactions, are covered in the Metapopulations and Multiple species vignettes.
An aside: masks
The processes above are unlikely to have consistent effects across
all vital rates or all classes in a population. To deal with this,
aae.pop is built around a concept of masks. Masks
are used to select specific elements of the population matrix, and only
these elements are altered by a given process.
Masks are paired with functions when defining all of the above processes. Masks tell R which cells to target, functions tell R what to do to these cells.
Several helper functions are included to define common masks. These
include the reproduction, survival, and
transition regions of the matrix discussed in the getting started vignette, as well as masks
to select an entire population matrix (all_cells) or
abundance vector (all_classes).
The masks defined in aae.pop return a
TRUE/FALSE matrix or vector that selects the
required cells. Masks are defined in this way because
aae.pop flattens the population matrix in all internal
calculations, which breaks cell-based subsetting (i.e., the
[i, j] R notation will not work). It is possible (but not
advised) to work around this. The discussion below
introduces one way to work around masks and highlights why this might
not be a good idea.
Back to demographic processes
A basic model
Let’s start with the basic model used in the Getting started vignette. This was a Leslie matrix with five age classes, with individuals reproducing from ages 3-5.
popmat <- rbind(
c(0, 0, 2, 4, 7), # reproduction from 3-5 year olds
c(0.25, 0, 0, 0, 0), # survival from age 1 to 2
c(0, 0.45, 0, 0, 0), # survival from age 2 to 3
c(0, 0, 0.70, 0, 0), # survival from age 3 to 4
c(0, 0, 0, 0.85, 0) # survival from age 4 to 5
)This is sufficient to start simulating population dynamics, using the
dynamics and simulate functions. However,
adding additional processes requires a few more steps first.
Demographic stochasticity
Random variation in individual outcomes is a key feature of most population models. This variation is most important (and influential) when populations are small, so that a few small events (e.g., several individuals failing to reproduce) can have a big effect on population outcomes.
Demographic stochasticity will be defined here with a single
mask and its corresponding function. The
simplest form of demographic stochasticity in this case is Poisson
variation around the expected number of individuals in the next
generation. This can be coded as:
demostoch_mask <- all_classes(popmat) # affects all classes
demostoch_fn <- function(x) {
rpois(length(x), lambda = x)
}Here, the mask selects all classes in the population
vector and the function takes this vector x
and returns random Poisson variates with mean equal to x.
Note that this function potentially allows the number of surviving
individuals in a class to exceed the number of available individuals
because the Poisson distribution does not have an upper bound. A
workaround for this, using the Binomial distribution, is covered in the
Beyond defaults vignette.
The mask/function pair can be combined into
a single object with the demographic_stochasticity
function.
demostoch <- demographic_stochasticity(
masks = demostoch_mask,
funs = demostoch_fn
)The resulting demostoch object can be passed directly to
dynamics, along with the population matrix. In turn, this
creates a dynamics object that can be used in
simulate.
# create population dynamics object
popdyn <- dynamics(popmat, demostoch)
# simulate population dynamics
sims <- simulate(popdyn, nsim = 100)
# plot the population trajectories
plot(sims, col = scales::alpha("#2171B5", 0.1))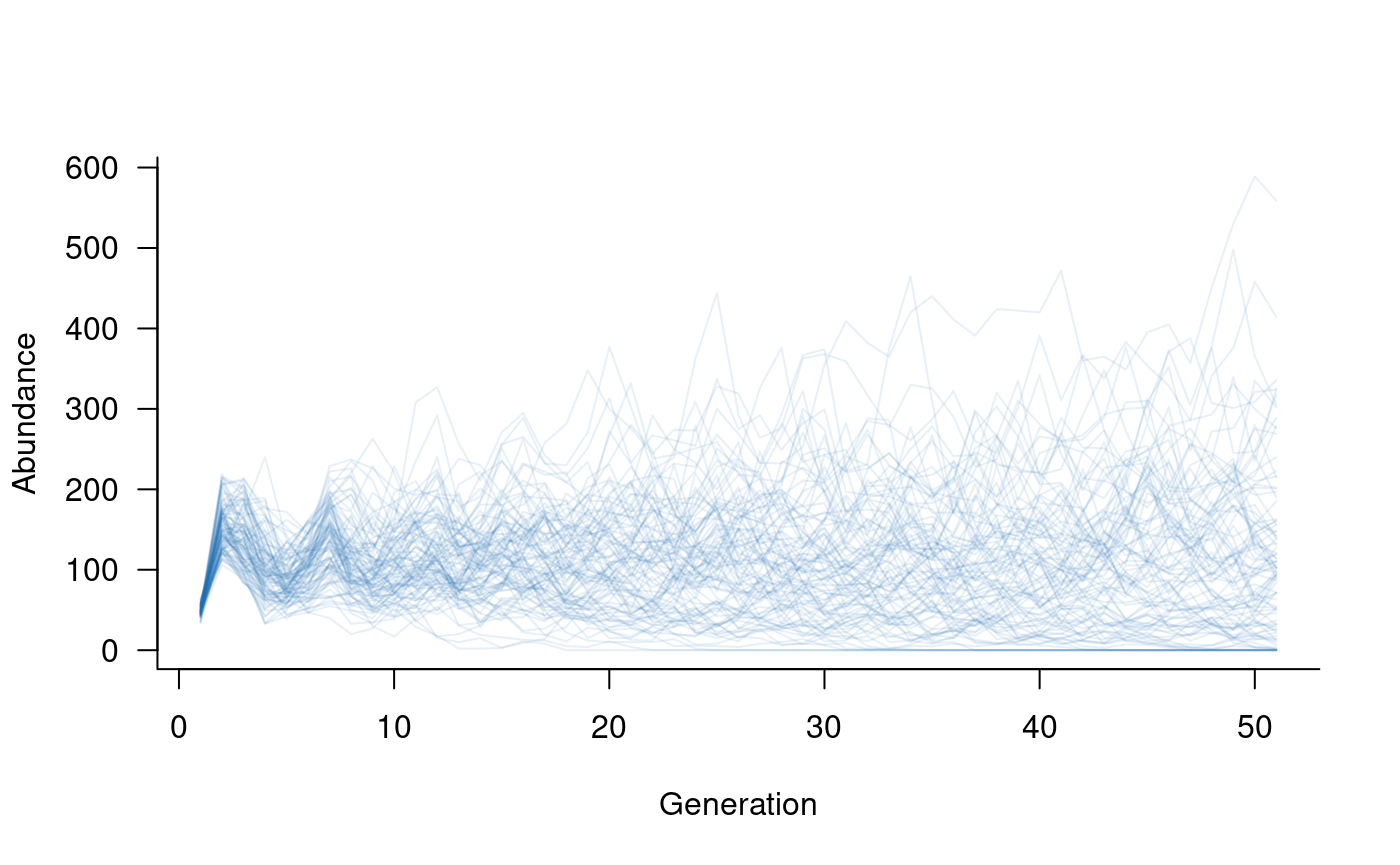
Environmental Stochasticity
Environmental stochasticity will be defined here with two masks and their corresponding functions. The simplest form of variation in reproduction is Poisson variation around the expected number of new individuals. This can be coded up as:
reproduction_mask <- reproduction(popmat, dims = 3:5) # only ages 3-5 reproduce
reproduction_fn <- function(x) {
rpois(length(x), lambda = x)
}Here, the mask selects the reproductive output of age
classes 3 to 5 in the population matrix and the function
takes this vector x and returns random Poisson variates
with mean equal to x.
The second mask/function pair will add
variation in survival outcomes. In this case, a simple form of variation
is to add or subtract some small value from the survival probabilities.
This can be coded up as:
transition_mask <- transition(popmat) # all classes this time
transition_fn <- function(x) {
# add a random deviation to x
deviation <- runif(length(x), min = -0.1, max = 0.1)
x <- x + deviation
# make sure the result isn't negative or greater than 1
x[x < 0] <- 0
x[x > 1] <- 1
# return the value
x
}Here, the mask selects all elements on the sub-diagonal
of the population matrix, and the function takes some
vector x and returns a new value with a deviation between
-0.1 and 0.1. There is one extra check in the function to make sure that
the new probabilities are still probabilities (i.e., still between 0 and
1).
These two mask/function pairs can be
combined into a single object with the
environmental_stochasticity function.
envstoch <- environmental_stochasticity(
masks = list(reproduction_mask, transition_mask),
funs = list(reproduction_fn, transition_fn)
)The resulting envstoch object can be passed directly to
dynamics, along with the population matrix. In turn, this
creates a dynamics object that can be used in
simulate.
# create population dynamics object
popdyn <- dynamics(popmat, envstoch)
# simulate population dynamics
sims <- simulate(popdyn, nsim = 100)
# plot the population trajectories
plot(sims, col = scales::alpha("#2171B5", 0.1))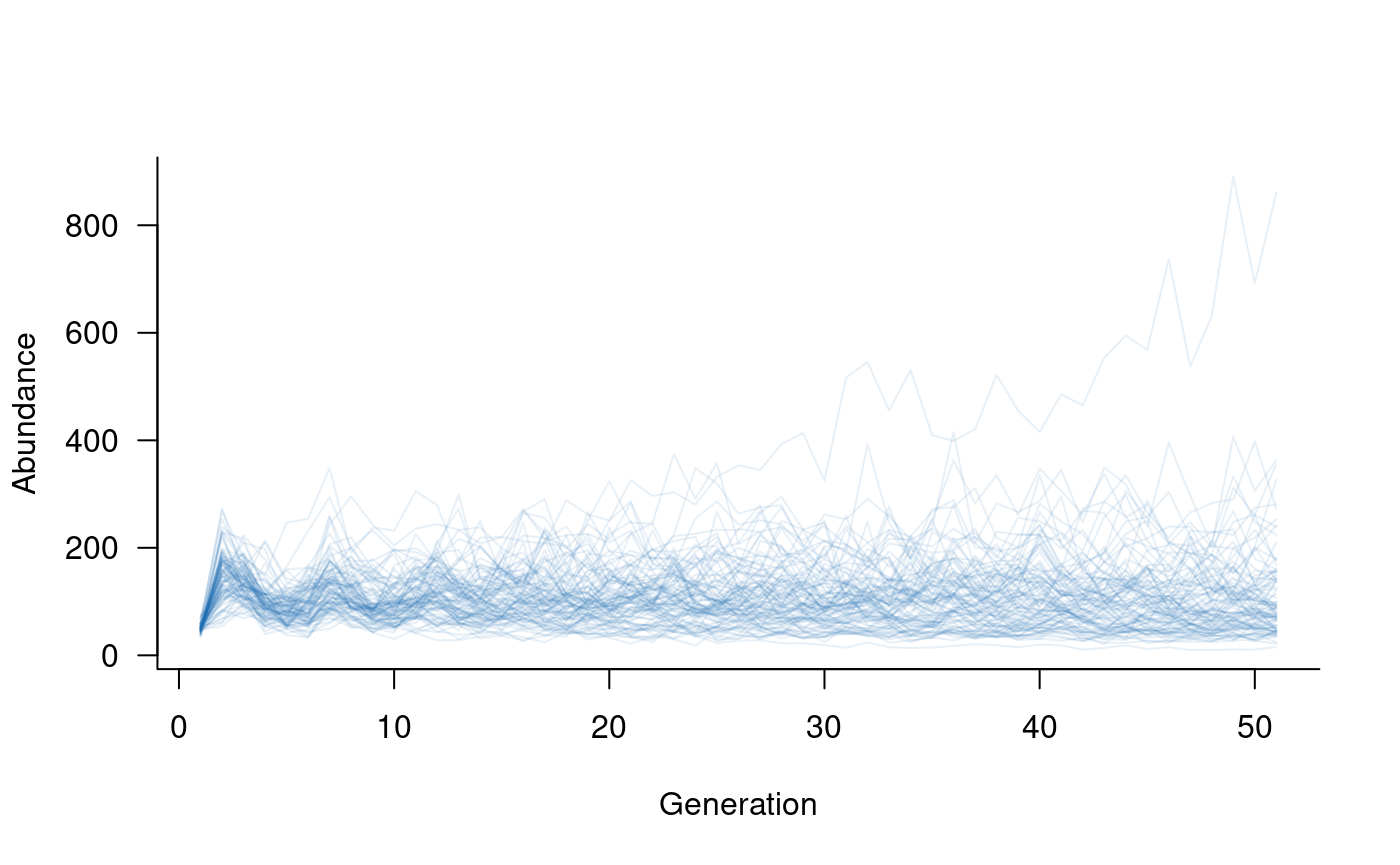
It is easy to include both environmental and demographic
stochasticity in the same model. The dynamics call simply
needs both envstoch and demostoch objects.
This is a case where the update function comes in handy.
Rather than re-defining the population dynamics object, the existing
version of popdyn (which included popmat and
envstoch) can simply be updated to include
demostoch:
# update population dynamics object
popdyn <- update(popdyn, demostoch)
# simulate population dynamics
sims <- simulate(popdyn, nsim = 100)
# plot the population trajectories
plot(sims, col = scales::alpha("#2171B5", 0.1))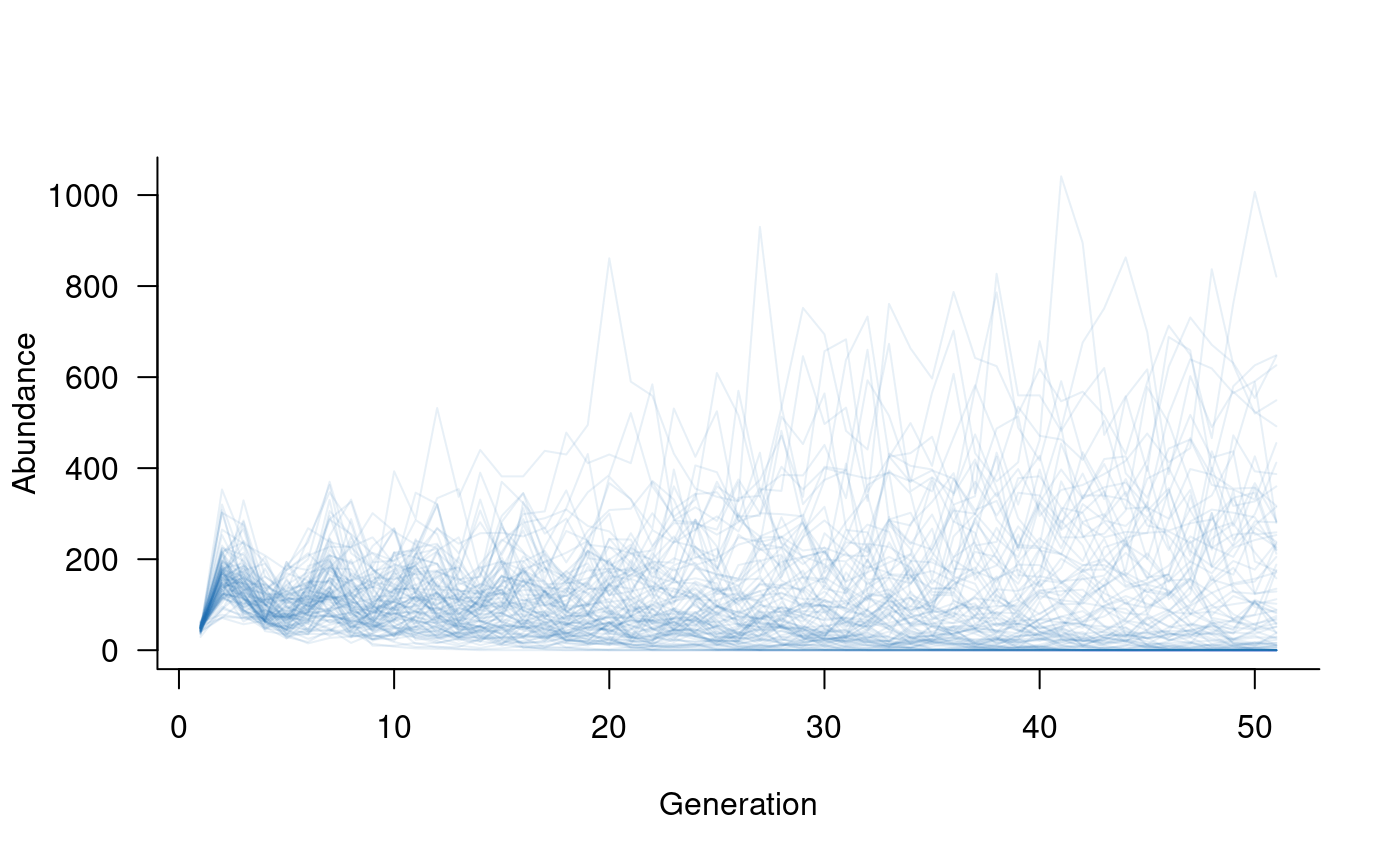
Density dependence
Density dependence occurs when vital rates or individual outcomes depend on population abundance. The most common form of density dependence in population ecology is negative density dependence, that is, a reduction in vital rates with increases in population abundance. Negative density dependence is typically observed as changes in reproduction due to, for example, increased competition for resources resulting in high mortality of new individuals.
Density dependence can be included in exactly the same way as
environmental stochasticity: a mask tells R which cells in
the population matrix are affected by abundances and a
function tells R what to do with these cells. In this case,
the function is passed the vital rates as well as the
vector of abundances in each population class.
aae.pop has pre-defined functions for two common forms
of density dependence: the Ricker model and the
Beverton-Holt model. The Ricker model assumes that mortality
rates of new individuals are proportional to adult population size due
to scramble competition (equal division of resources). The
Beverton-Holt model assumes that mortality rates of new individuals are
linearly dependent on the number of individuals due to contest
competition (unequal division of resources). Importantly, the
Ricker model is overcompensatory, which means it can increase
mortality rates to the point of complete mortality. This does not occur
under the Beverton-Holt model.
In aae.pop, both models are specified with one
parameter, k, that represents the carrying
capacity of the population. Both functions include one extra
argument, exclude, which allows estimates of carrying
capacity to be defined for a subset of population classes (e.g., adult
abundances only). A Ricker model can be specified as follows:
# specify a Ricker model for density dependence
dd <- density_dependence(
masks = reproduction(popmat, dims = 3:5), # only adults reproduce
funs = ricker(k = 40, exclude = 1:2) # set k based on adult abundances
)
# update the population dynamics object to include density dependence
popdyn <- update(popdyn, dd)
# simulate population dynamics
sims <- simulate(popdyn, nsim = 100)
# plot the population trajectories
plot(sims, col = scales::alpha("#2171B5", 0.1))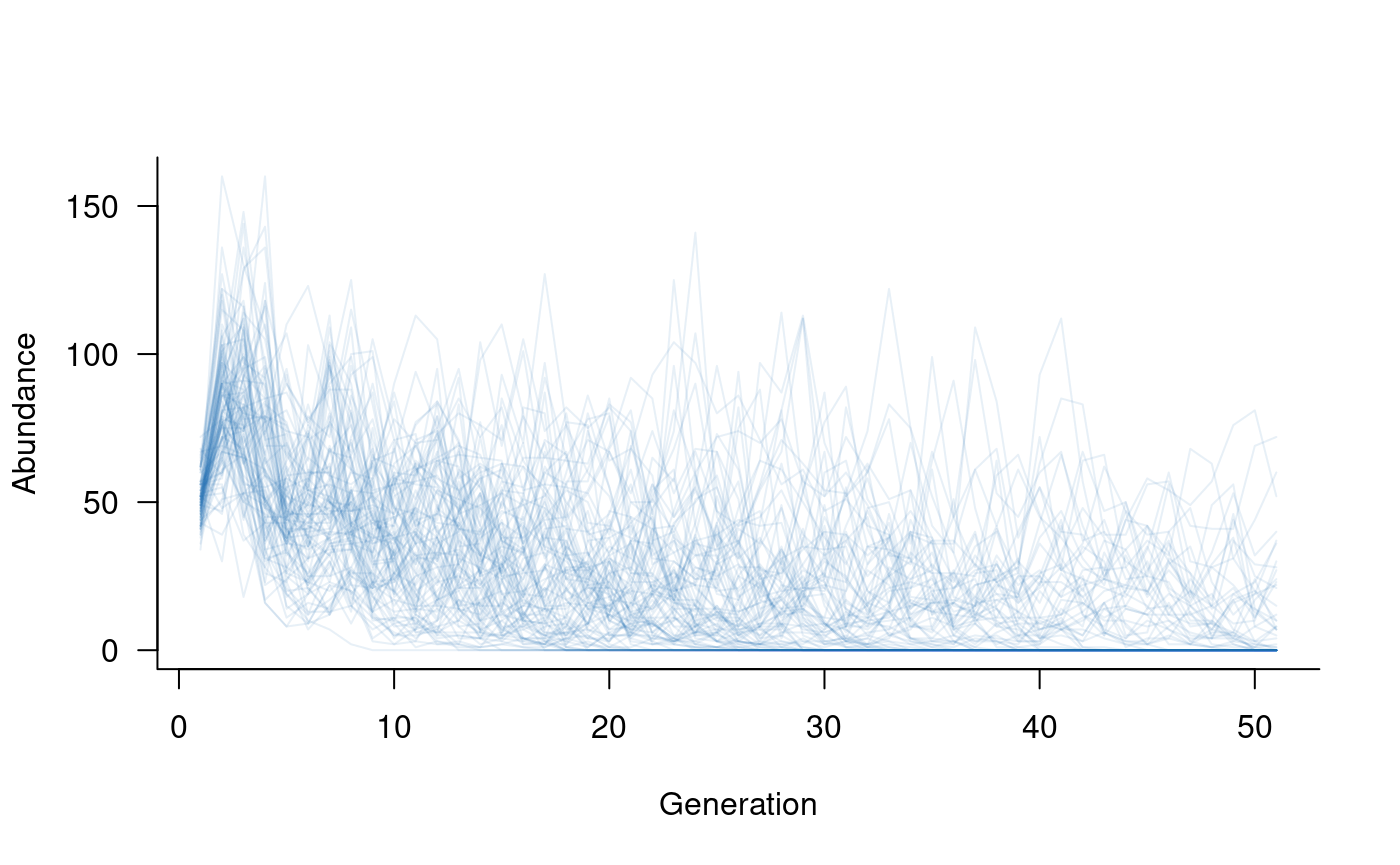
Density dependence can take many other forms. These forms may include positive density dependence (e.g., Allee effects) or may affect adult abundances as well as reproduction. An example of the former is included in the Macquarie perch worked example. The next section introduces an example of the latter.
A different form of density dependence
Density dependence is most commonly assumed to affect only the new
individuals entering the population. However, it is possible that
density dependence also affects adults, for example, when high
abundances limit access to suitable habitat. Effects on adult survival
could be modelled using the approach outlined in the previous section,
with transition or survival masks alongside
the reproduction mask.
An alternative approach is to model density dependence through its direct effects on population abundances. Although not linked directly to vital rates (e.g., survival), this approach can be easier to implement and can capture processes that do not directly affect vital rates, such as fishing, hunting, or logging.
The density_dependence_n function defines this form of
density dependence. In this case, the mask needs to select
the relevant classes in the population, and the function
takes only one argument, the vector of population abundances. This
approach can be implemented as follows:
# specify density dependence that removes 10 % of adults in each generation
dd_n <- density_dependence_n(
masks = all_classes(popmat, dims = 3:5), # want to focus on adults
funs = function(n) 0.9 * n # define in-line function to return
# 90 % of adult population
)
# create a new population dynamics object
popdyn <- dynamics(popmat, envstoch, demostoch, dd_n)
# simulate population dynamics
sims <- simulate(popdyn, nsim = 100)
# plot the population trajectories
plot(sims, col = scales::alpha("#2171B5", 0.1))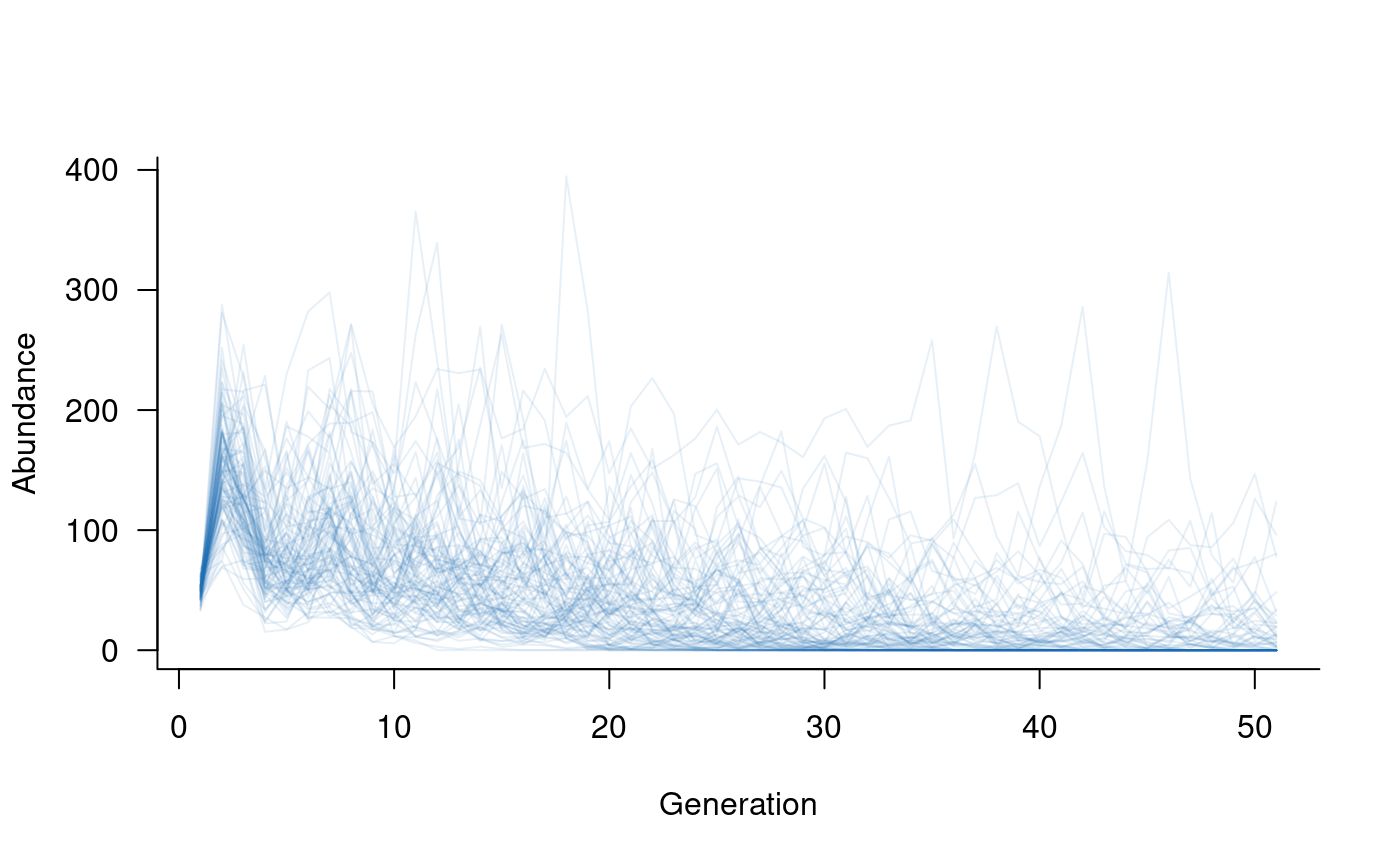
Covariates
Population dynamics often depend on external factors
(covariates, here). aae.pop uses the
mask/function approach described above to
include the effects of covariates on vital rates. The
function takes the vital rates as the first argument,
followed by any arguments required to specify covariate values or their
effects. An example illustrates this most clearly:
# set up 20 years of covariates, such as proportion of available nesting sites
nesting <- runif(20, min = 0.5, max = 1.0) # 50 % to 100 % of total sites available in each year
# define the mask
covar_mask <- reproduction(popmat, dims = 3:5) # assume nesting sites only affect reproduction
# define a function that links vital rates to the covariates
covar_fn <- function(x, nests) {
x * nests # really simple function, assume the proportion of successful reproduction
# attempts is equal to the proportion of nests
}
# combine this into a covariates term
covs <- covariates(covar_mask, covar_fn)
# create population dynamics object (without density dependence)
popdyn <- dynamics(popmat, envstoch, demostoch, covs)
# simulate population dynamics
sims <- simulate(
popdyn,
nsim = 100,
args = list(covariates = format_covariates(nesting))
)
# plot the population trajectories
plot(sims, col = scales::alpha("#2171B5", 0.1))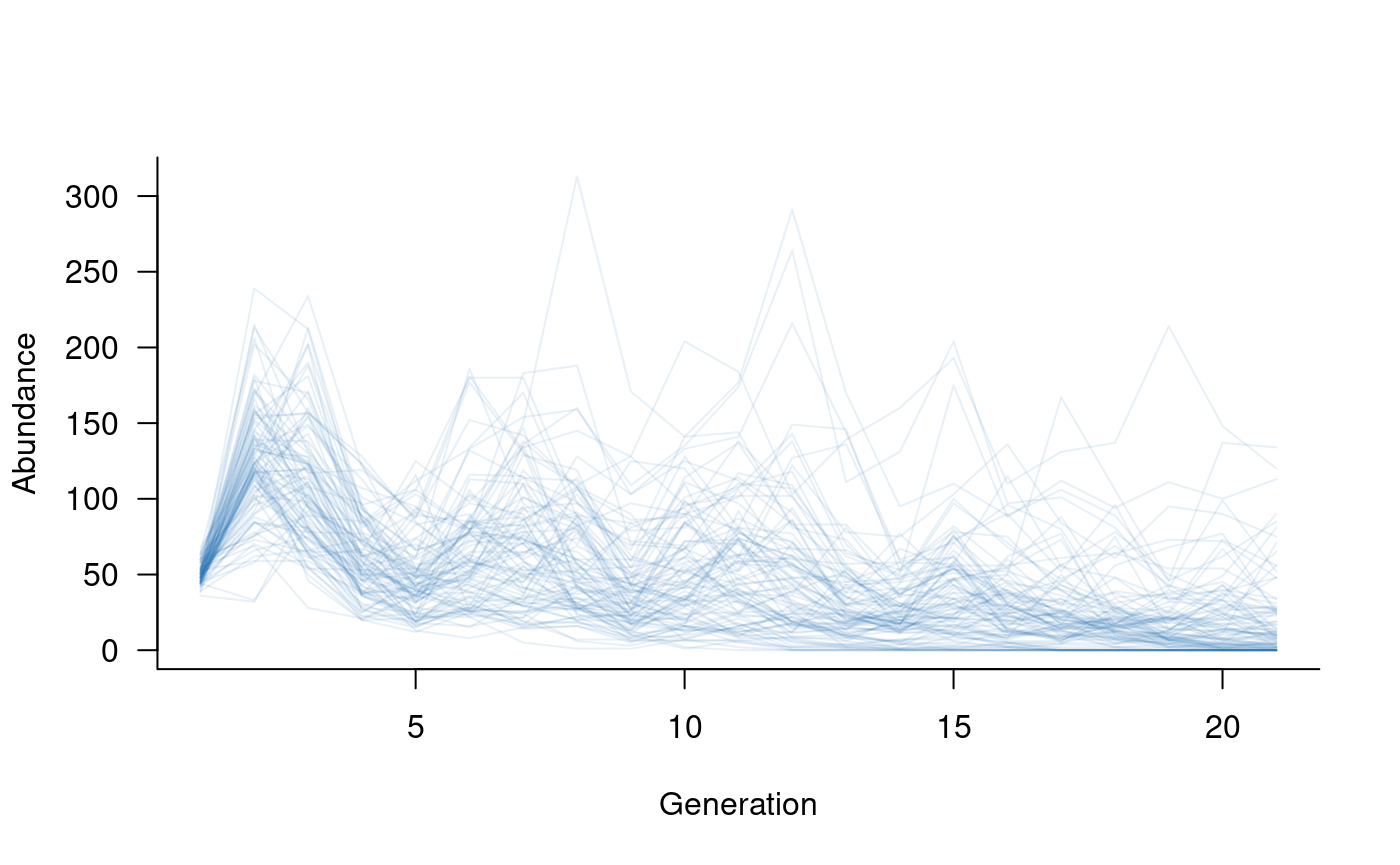
Specifying a covariates term does not automatically
include covariates in the model. Note that the nesting
variable also had to be passed to simulate via the
args argument. The reason for this is that it allows a
single population dynamics object (popdyn, above) to be
used with multiple different sets of covariates, without re-compiling
the dynamics object each time. The
format_covariates function is included to format covariate
values and any auxiliary (static) variables.
aae.pop assumes that covariates change
through time, so a consequence of specifying covariates is that the
vector/matrix of covariates determines the number of simulated time
steps (n_time). In the above example, there were 20 values
of nesting, which translates to 21 time steps (initial
condition plus 20 updates).
It is assumed that covariates can be passed as a vector, matrix, or
data.frame, with one element or row for each time step. More complex
covariate terms are possible, such as dynamic arguments
that change through time or functions that specify arguments based on
the current state of the population. These terms can be passed to
simulate via the args argument but must follow
specific rules described in the Passing
arguments vignette.
What if I don’t want to use masks?
The mask/function approach is central to
aae.pop. This approach allows multiple functions to be
combined into a single term and makes it easier to keep track of (and
update) individual functions or masks. A secondary reason for this
approach is computational. Rarely will any demographic processes act on
the entire population matrix. When dealing with large matrices (e.g.,
50-100 classes), it’s much more efficient to pass small parts of the
matrix than the entire matrix.
There might be situations where the entire population matrix does
need to be modified by a given process. This is still supported in
aae.pop through the all_cells
mask. However, it isn’t possible to subset the matrix
within a function using R’s standard [i, j]
notation. This is because the functions within aae.pop
receive a flattened (and masked) version of the population matrix, which
actually looks like:
# reproduction mask
popmat[reproduction(popmat, dims = 3:5)]## [1] 2 4 7or
# transition mask
popmat[transition(popmat)]## [1] 0.25 0.45 0.70 0.85or
# all elements
popmat[all_cells(popmat)]## [1] 0.00 0.25 0.00 0.00 0.00 0.00 0.00 0.45 0.00 0.00 2.00 0.00 0.00 0.70 0.00
## [16] 4.00 0.00 0.00 0.00 0.85 7.00 0.00 0.00 0.00 0.00If it’s essential to use [i, j] subsetting inside a
function, a workaround is to reconstruct the matrix within the function
by passing the dimensions through the args argument in
simulate. This might look a bit like:
# define a function
no_mask_fn <- function(x, dim) {
# reconstruct matrix
x <- array(x, dim = dim)
# change elements with [i, j] notation
x[2, 1] <- 0.6 * x[2, 1]
x[3, 2] <- 1.25 * x[3, 2]
# return
x
}
# set this up as a form of environmental stochasticity
envstoch <- environmental_stochasticity(
masks = all_cells(popmat), # pass the entire matrix
funs = no_mask_fn # use the no-mask function
)
# create population dynamics object (without density dependence)
popdyn <- dynamics(popmat, envstoch)
# simulate population dynamics
sims <- simulate(
popdyn,
nsim = 100,
args = list(environmental_stochasticity = list(dim = dim(popmat)))
)
# plot the population trajectories
plot(sims, col = scales::alpha("#2171B5", 0.1))